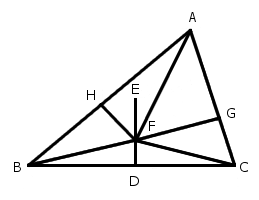
Lewis Carroll offered this proof that all triangles are isosceles:

Let ABC be any triangle. Bisect BC at D, and from D draw DE at right angles to BC. Bisect the angle BAC.

(1) If the bisector does not meet DE, they are parallel. Therefore the bisector is at right angles to BC. Therefore AB = AC, i.e., ABC is isosceles.

(2) If the bisector meets DE, let them meet at F. Join FB, FC, and from F draw FG, FH, at right angles to AC, AB.

Then the triangles AFG, AFH are equal, because they have the side AF in common, and the angles FAG, AGF equal to the angles FAH, AHF. Therefore AH = AG, and FH = FG.

Again, the triangles BDF, CDF are equal, because BD = DC, DF is common, and the angles at D are equal. Therefore FB = FC.

Again, the triangles FHB, FGC are right-angled. Therefore the square on FB = the [sum of the] squares on FH, HB; and the square on FC = the [sum of the] squares on FG, GC. But FB = FC, and FH = FG. Therefore the square on HB = the square on GC. Therefore HB = GC. Also, AH has been proved equal to AG. Therefore AB = AC; i.e., ABC is isosceles.

Therefore the triangle ABC is always isosceles. Q.E.D.