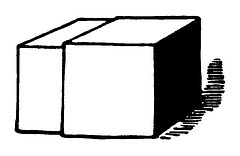
A puzzle from Henry Dudeney:
I had two solid cubes of lead, one very slightly larger than the other, just as shown in the illustration. Through one of them I cut a hole (without destroying the continuity of its four sides) so that the other cube could be passed right through it. On weighing them afterwards it was found that the larger cube was still the heavier of the two! How was this possible?
|
SelectClick for Answer |
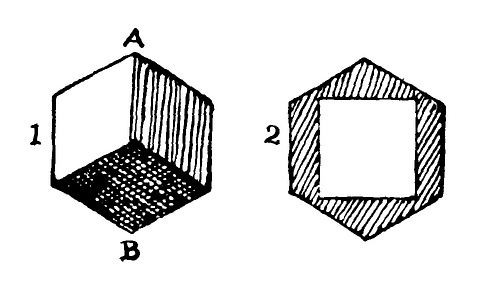
It is a curious fact that a cube can be passed through another cube of smaller dimensions. Suppose a cube to be raised so that its diagonal AB is perpendicular to the plane on which it rests, as in Figure 1. Then the resulting projection will be a regular hexagon, as shown. In Figure 2 the square hole is cut for the passage of a cube of the same dimensions. But it will be seen that there is room for cutting a hole that would pass a cube of even larger dimensions. Therefore, the one through which I cut a hole was not, as the reader may have hastily supposed, the larger one, but the smaller! Consequently, the larger cube would obviously remain the heavier. This could not happen if the smaller were passed through the larger.
|


