Alice and Bob are two infinitely intelligent logicians. Each has a number drawn on their forehead. Each can see the other’s number but not their own. Each knows that both numbers are positive integers. An observer tells them that the number 50 is either the sum or the product of the two numbers. Alice says to Bob, “I do not know my number,” and Bob replies, “I do not know my number either.” What is Alice’s number?
Moment

It is related of the Socratic philosopher Aristippus that, being shipwrecked and cast ashore on the coast of the Rhodians, he observed geometrical figures drawn thereon, and cried out to his companions: ‘Let us be of good cheer, for I see the traces of man.’
— Vitruvius, De architectura
Close Reading
Teaching at Cornell in the 1950s, Vladimir Nabokov offered a European fiction course whose exam questions could be distressingly broad or pitilessly specific — some examples are given in an appendix to Lectures on Literature:
Bleak House
- Why did Dickens need to give Esther three suitors (Guppy, Jarndyce, and Woodcourt)?
- If you compare Lady Dedlock and Skimpole, which of them is the author’s greater success?
- Discuss the structure and style of Bleak House.
- Discuss John Jarndyce’s house. (Mangles? Surprised birds?)
- Discuss the visit to Bell Yard (Neckett’s children; and Mr. Gridley).
- Give at least four examples of the “child theme” in Bleak House.
- What kind of place was Bleak House — give at least four descriptive details.
- Where was Bleak House situated?
- How is the “bird theme” linked up with Krook?
- How is the “fog theme” linked up with Krook?
- Whose style are we reminded of when Dickens raises his voice?
- The social side (“upper class” versus “lower class” etc.) is the weakest one in Bleak House. Who was Mr. George’s brother? What part did he play? Should a major reader skip those pages, even if they are weak?
- Follow Mr. Guppy through Bleak House.
Madame Bovary
- Describe briefly Flaubert’s use of the counterpoint technique in the County Fair scene.
- There are numerous thematic lines in Madame Bovary, such as “Horse,” “Plaster Priest,” “Voice,” “The Three Doctors.” Describe these four themes briefly.
- Discuss Flaubert’s use of the word “and.”
- What character in Madame Bovary behaves in very much the same way as a character in Bleak House does under somewhat similar circumstances? The thematic clue is: “devotion.”
- Is there a Dickensian atmosphere about Flaubert’s description of Berthe’s infancy and childhood? (Be specific.)
- The features of Fanny Price and Esther are pleasantly blurred. Not so with Emma. Describe her eyes, hair, hands, skin.
- Would you say that Emma’s nature was hard and shallow?
- Would she prefer a landscape peopled with ruins and cows to one that contained no allusions to people?
- Did she like her mountain lakes with or without a lone skiff?
- What had Emma read? Name at least four works and their authors.
In his annotated copy of The Metamorphosis, Nabokov, a trained entomologist, observed that “A regular beetle has no eyelids and cannot close its eyes” — and thus Gregor Samsa is “a beetle with human eyes.”
Rebus

A Brooklyn bookseller distributed this card during the 1880 U.S. presidential race between James Garfield and Winfield Scott Hancock. What does it say?
Unquote
“What is research but a blind date with knowledge?” — Will Henry
Making the Case
Alexander Shapovalov suggested an unusual coin-weighing problem for the sixth international Kolmogorov math tournament in 2007:
A judge is presented with 80 coins that all look the same, knowing that there are either two or three fake coins among them. All the real coins weigh the same and all the fake coins weigh the same, but the fake coins are lighter than the real ones.
A lawyer knows that there are exactly three fake coins and which ones they are. The lawyer must use a balance scale to convince the judge that there are exactly three fake coins and that it is impossible for there to be only two fake coins. She is bound by her contract not to reveal any information about any particular coin. How should she proceed?
The lawyer might try dividing the 80 coins into three groups of 26, each group containing one fake coin, with two coins left over. With two weighings she could then show that the three groups have the same weight. From this the judge could conclude that either (a) there are 3 fake coins, one in each group, or (b) there are 2 fake coins, both in the leftover group. The lawyer could then weigh one of the leftover coins against a real coin taken from one of the three groups, to show that these balance. This would prove to the judge that there are 3 fake coins (because if there were only 2 then possibility (b) above would be ruled out). However, this strategy is “indiscreet” — it would reveal to the judge the true character of each of the leftover coins, which the lawyer has pledged not to do. How should she proceed instead?
The Immortal Bridge

This rock formation, formed possibly thousands of years ago, spans a chasm on Mount Tai, one of the Five Great Mountains of China.
It’s said that anyone who crosses the bridge will live forever.
Endless Variety
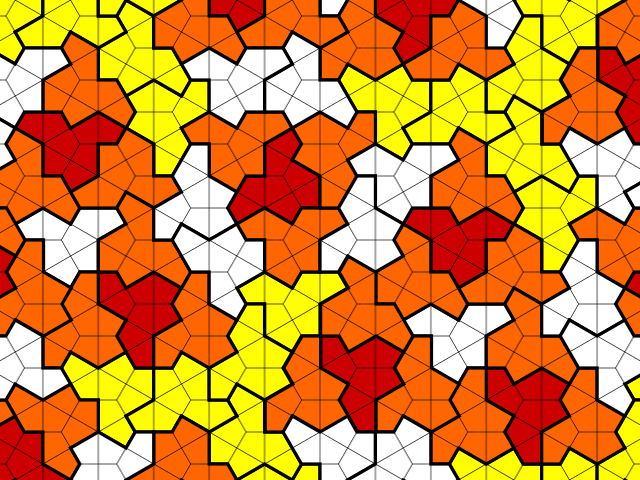
In 2022, amateur mathematician David Smith discovered a remarkable tile that will cover an infinite plane but only in a nonperiodic way.
This solves an open problem in mathematics — for years researchers had been seeking an aperiodic monotile, or “einstein,” from the German for “one stone.”
Technically Smith’s tile, known as the “hat,” must be used in combination with its mirror image. But last year his team found another nonperiodic tile, known as the spectre, which is strictly chiral — that is, not only will it tile the plane without its mirror image, but it must be used in that way.
Nighttide

“Did anyone ever have a boring dream?” — Ralph Hodgson
Hope Springs Eternal

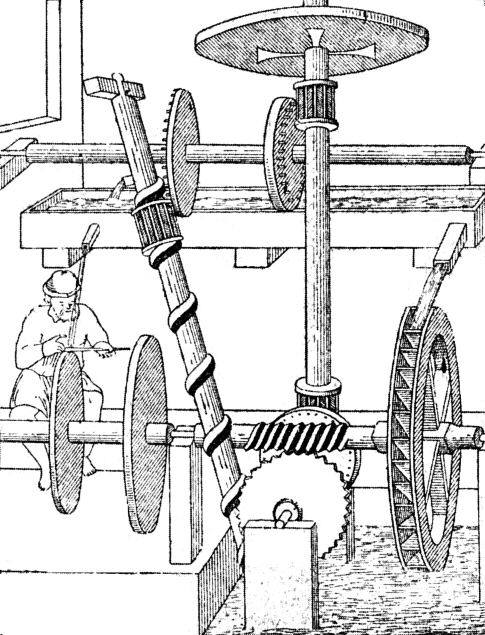
Ulrich von Cranach of Hamburg devised this perpetual motion machine in 1664, offering it to drive pumps in mines. An Archimedean screw raises a succession of iron balls that then descend by a wheel that turns the screw.
Robert Fludd had proposed a water mill in 1618 that used essentially the same design. The anonymous variant below dates from the Middle Ages.