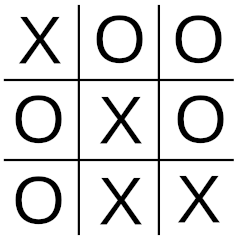
A puzzle by Paul Hoffman, from Science Digest. Could this game ever have resulted from a strict adherence to the rules of tic-tac-toe (noughts and crosses)?

A puzzle by Paul Hoffman, from Science Digest. Could this game ever have resulted from a strict adherence to the rules of tic-tac-toe (noughts and crosses)?

At the far end of the room was an easel on which lay a painting, not quite finished, depicting the Empire of Flora, the original of which was by Poussin. The painter’s palette and brushes were left beside the painting. Above it, on a piece of paper, was a red chalk drawing of the painting. … I examined all of this, both from afar and up close, without finding anything worth dwelling on; but my surprise was unparalleled when, upon trying to take the drawing, I discovered that it was all a fabrication, and that the whole thing was a single painting entirely in oil. … If I were in a position to possess this painting, I would gladly give ten thousand francs for it.
From Charles de Brosses, L’Italie il y a cent ans., 1836. The painting was Antoine Fort-Bras’ 1686 Le Chevalet du peintre, now at the Calvet Museum in Avignon. Flemish painter Cornelius Gijsbrechts had pulled the same trick a decade earlier.
A problem from Joseph Madachy’s Mathematics on Vacation (1966):
When Bert was just one year younger than Bill was when Ben was half as old as Bill will be 3 years from now, Ben was twice as old as Bill was when Ben was 1/3 as old as Bert was 3 years ago. But, when Bill was twice as old as Bert, Ben was 1/4 as old as Bill was one year ago.
“Ignoring odd months and considering that Bert has passed the half-century mark, it will be no problem to find out how old these three friends are.”
As the U.S. tariff act of June 6, 1872, was being drafted, planners intended to exempt “Fruit plants, tropical and semi-tropical for the purpose of propagation or cultivation.”
Unfortunately, as the language was being copied, a comma was inadvertently moved one word to the left, producing the phrase “Fruit, plants tropical and semi-tropical for the purpose of propagation or cultivation.”
Importers pounced, claiming that the new phrase exempted all tropical and semi-tropical fruit, not just the plants on which it grew.
The Treasury eventually had to agree that this was indeed what the language now said, opening a loophole for fruit importers that deprived the U.S. government of an estimated $1 million in revenue. Subsequent tariffs restored the comma to its intended position.
Visiting Lord Byron in 1821, Percy Shelley wrote to his friend Thomas Love Peacock:
“Lord Byron’s establishment consists, besides servants, of ten horses, eight enormous dogs, three monkeys, five cats, an eagle, a crow, and a falcon; and all these, except the horses, walk about the house, which every now and then resounds with their unarbitrated quarrels as if they were the masters of it.”
He added in a postscript: “I have just met on the grand staircase five peacocks, two guinea-hens, and an Egyptian crane. I wonder who all these animals were, before they were changed into these shapes.”
In 1818, English zoologist William Elford Leach named nine new genera of parasitic isopods: Anilocra, Canolira, Cirolana, Conilera, Lironeca, Nelocira, Nerocila, Olencira, and Rocinela.
Each of these is an anagram of the name Caroline (or its Latinized form Carolina). But Leach was not married and had no known relationship with any woman of that name.
The genera stand as a “tantalizing puzzle for posterity.” More here.
[Thomas Chaloner] had a trick sometimes to goe into Westminster hall in a morning in Terme time, and tell some strange story (sham), and would come thither again about 11 or 12 to have the pleasure to heare how it spred; and sometimes it would be altered, with additions, he could scarce knowe it to be his owne.
— John Aubrey, Brief Lives, 1697
George Washington’s teenage journal contains this love acrostic:
From your bright sparkling Eyes, I was undone;
Rays, you have, more transparent than the sun,
Amidst its glory in the rising Day,
None can you equal in your bright arrays;
Constant in your calm and unspotted Mind;
Equal to all, but will to none Prove kind,
So knowing, seldom one so Young, you’l Find.
Ah! woe’s me, that I should Love and conceal,
Long have I wish’d, but never dare reveal,
Even though severely Loves Pains I feel;
Xerxes that great, was’t free from Cupids Dart,
And all the greatest Heroes, felt the smart.
Reading the first letter of each line spells FRANCES ALEXA. Who was this? Possibly the subject’s full name was Frances Alexander and Washington hadn’t finished the poem.
“When Dr. Barton Warren was informed that Dr. Vowel was dead, he exclaimed, ‘What! Vowel dead? Well, thank heaven it was neither you nor I.'”
— William S. Walsh, Handy-Book of Literary Curiosities, 1892