“If anything is possible, then it is possible to prove that something is impossible. And if it is possible to prove that something is impossible, then necessarily, something is impossible.”
— Roy Sorensen, Vagueness and Contradiction, 2001
Misc
- Asked to invent the perfect bestselling title, Bennett Cerf suggested Lincoln’s Doctor’s Dog.
- The two most common birthdates for Nobel laureates are May 21 and February 28 (seven apiece).
- ALASKA is the only U.S. state name that can be typed on a single row of keys on a standard typewriter.
- 13177388 = 71 + 73 + 71 + 77 + 77 + 73 + 78 + 78
- “I don’t know much about medicine, but I know what I like.” — S.J. Perelman
Dream Time
In 1898 J.W. Dunne was staying at a hotel in Sussex when he dreamed he was arguing with one of the waiters. He was claiming that it was 4:30 in the afternoon, and the waiter maintained it was 4:30 in the morning. “With the apparent illogicality peculiar to all dreams, I concluded that my watch must have stopped; and, on extracting that instrument from my waistcoat pocket, I saw, looking down on it, that this was precisely the case. It had stopped — with the hands at half-past four. With that I awoke.”
He lit a match to see whether his watch really had stopped. It was not by his bedside, but after some hunting he found it lying on a chest of drawers. It had stopped, and the hands stood at 4:30. Noting the coincidence, he wound the watch and returned to bed.
On coming downstairs the next morning, he went to the nearest clock in order to restore the watch to the correct time. He expected to find it off by several hours, as he supposed it had stopped during the previous afternoon and was rewound in the middle of the night.
But “to my absolute amazement I found that the hands had lost only some two or three minutes, about the amount of time which had elapsed between my waking from the dream and rewinding the watch.”
In other words, the dream watch and the waking watch had stopped at the same moment. Possibly the sleeping Dunne had sensed that his watch’s familiar ticking had stopped, and this had informed his dream. “But — how did I come to see, in that dream, that the hands stood, as they actually did, at half-past four?”
Unquote
“Nothing is so silly as the expression of a man who is being complimented.” — André Gide
A Look Ahead
In 1888 New York journalist David Goodman Croly published Glimpses of the Future, a collection of predictions “to be read now and judged in the year 2000.” Excerpts:
- “The accumulation of wealth in a few hands, which is steadily going on, will unquestionably lead to a grave agitation which may have vital consequences on the future of the country. I am quite sure that the American of the twentieth century will not consent to live under a merely selfish plutocracy.”
- “Exclusive lawyer rule will yet create violent disturbance. Our whole machinery of justice is out of gear, for it is becoming more costly and inefficient. … The legal machinery grows yearly more inefficient and wasteful of time and money. Vigilance committees will exist in every part of the country if this state of things continues.”
- “Marriage is no longer a religious rite even in Catholic countries, but a civil contract, and the logical result would seem to be a state of public opinion which would justify a change of partners whenever the contracting couple mutually agreed to separate.”
- “If the aërostat should become as cheap for travellers as the sailing vessel, why may not man become migratory, like the birds, occupying the more mountainous regions and sea-coast in summer and more tropical climes in winter? Of course all this seems very wild, but we live in an age of scientific marvels, and the navigation of the air, if accomplished, would be the most momentous event of all the ages.”
- “There will be a sub-city [in New York] under the surface of the ground for conveying people, not only from the Battery to the City Hall Park, but also from the East to the North River.”
- “True, the [chromolithograph] of to-day is looked upon as crude and inartistic; but I venture to predict that it will be so far perfected as to allow any well-to-do family to have art galleries of their own, in which will be found reproductions of all the great paintings of the ancient and modern world. The crowning glory of our age will be when the highest art is brought within the reach of the poorest purse.”
- “[In the novel of the future,] Robert Elsmere, Catherine Langham, and the other individuals, would all be reproduced pictorially. This would dispense with a great deal of description, and much of the verbiage could be cut out. Then the reader’s conception of the characters would necessarily be much more vivid. Nor is this all. Why should not a number of graphophones be made use of, giving the words of the various conversations in the tones they would naturally use? An author then would employ a number of men and women of various ages to personate his characters. They would be like the models of an artist.”
“I have no notion of being able to tell what the future has in store for us,” he wrote. “I propose simply to take up such matters as are of everyday importance, and try to think out the future with regard to them.”
Drawing Blanks
In 2002, Russian magnate Vladimir O. Potanin paid $1 million for Kazimir Malevich’s 1915 painting Black Square. “‘All paintings are pictures’ would have been a strong candidate for a necessary truth until Malevich proved it false,” wrote Arthur Danto of the inscrutable black canvas. Malevich himself had said, “It is not painting; it is something else.”
In The Hunting of the Snark, the Bellman guides his party across the Ocean with “a map they could all understand”:
“What’s the good of Mercator’s North Poles and Equators,
Tropics, Zones, and Meridian Lines?”
So the Bellman would cry: and the crew would reply
“They are merely conventional signs!
“Other maps are such shapes, with their islands and capes!
But we’ve got our brave Captain to thank”
(So the crew would protest) “that he’s bought us the best —
A perfect and absolute blank!”
While an architecture student at Cornell in the 1920s, practical joker Hugh Troy was given 48 hours to render “a conception of what a brightly floodlighted hydroelectric plant might look like at night.” “Though Hugh was overloaded with other work, he got his drawing in on time,” remembered classmate Don Hershey. He called it Hydroelectric Plant at Night (Fuse Blown):
In 1967 British artists Terry Atkinson and Michael Baldwin produced a “map of itself,” a “map of an area of dimensions 12″ x 12″ indicating 2,304 1/4″ squares”:
Katharine Harmon, in The Map as Art, writes that this is one of a series of maps “revealing only what they wished to show and jettisoning the rest — drawing attention to what cartographers have always done.”
(Thanks, Tristram.)
Two Squares
Retired Pittsburgh math teacher Walter W. Horner devised this doubly magic square in 1955:
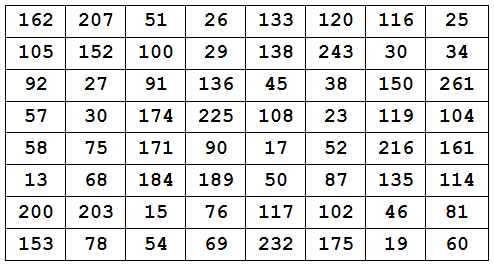
Each row, column, and long diagonal produces both a sum of 840 and a product of 2058068231856000.
And Rodolfo Marcelo Kurchan of Buenos Aires discovered this remarkable square in 1991:
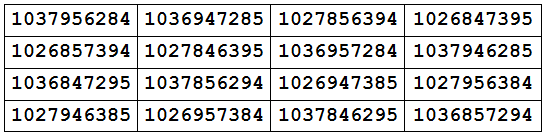
Each number contains all 10 digits — and so does the magic sum, 4129607358.
Being and Nothingness
There was a shoemaker in Paris, which was a widower, and he was not very wise. Of him Scogin bought all his shooes, and on a time Scogin came to the shoemaker’s house to speak with him. The shoemaker was at dinner, and bad his maid say that he was not at home. Scogin, by the maid’s answer, perceived that her master was within, but for that time dissembled the matter, and went home. Shortly after, the shoomaker came to Scogin’s chamber, and asked for him. Scogin, hearing the shoomaker enquire for him, said aloud: I am not at home. Then sayd the shoomaker: what, man, think you that I know not your voice? Why, said Scogin, what an unhonest man you are! When I came to your house, I beleeved your maid that said you were not at home, and you will not beleeve me mine owne selfe.
— Scoggin’s Jests, 1626
Moving Violation
I want to take my one-piece bass flute on the train, but it’s 1.7 meters long and the baggage man won’t take any item whose greatest dimension exceeds 1 meter. What can I do?
Lettershifts
Advance each letter in BANJO four places through the alphabet and you get FERNS:
Advance MANFUL seven places and you get THUMBS. Surely this means something.