
A garrulous barber asked the Macedonian king Archelaus, “How shall I cut your hair?”
He answered, “In silence.”
(From Plutarch.)

A garrulous barber asked the Macedonian king Archelaus, “How shall I cut your hair?”
He answered, “In silence.”
(From Plutarch.)
A “Home Counties version” of the Lord’s Prayer:
Our Farnham which art in Hendon, Harrow be thy Name. Thy Kingston come. Thy Wimbledon in Erith, as it is in Heston. Give us this day our Leatherhead. And forgive us our Westminsters, as we forgive them that Westminster against us. And lead us not into Thames Ditton, but deliver us from Ealing. For thine is the Kingston, the Purley, and the Crawley, for Iver and Iver. Crouch End.
I don’t think anyone knows who wrote it. See The Author’s Tale.

On the Bench his lips would often be seen to move, but no sound proceeding from them would be heard by the Bar. The associate sitting beneath him could tell another tale. … ‘What a damned fool that man is!’ — then, after an interval, ‘Eh, not such a damned fool as I thought;’ then another interval. ‘Egad, it is I that was the damned fool.’
— J.B. Atlay on Lord Lyndhurst, in The Victorian Chancellors, 1906
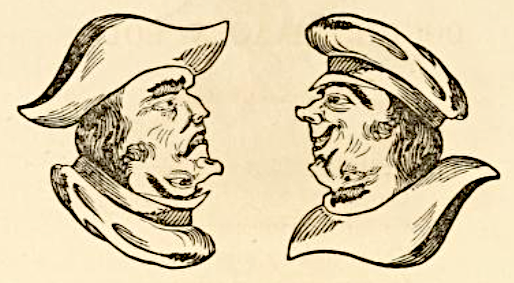
An acrostic by Robert Blackwell, 1868:
Turn this book and at us look,
Heed our features, too,
Expressive, fine, our faces shine,
To please such folks as you;
With heads but four, we want no more,
Our eyes give us no light;
Our ears are deaf, but yet no grief
Disturbs us day nor night;
Deprived of feet we can not walk
In houses where we go,
The reason why we do not sigh,
Is left for you to know.
Ever free from care are we,
So turn this book, and at us look.
Reading the first letter in each line produces the phrase “The Two Oddities.” Inverting the book gives the answer to the riddle: The “four heads” are actually one carefully devised figure — each face is the other upside down:
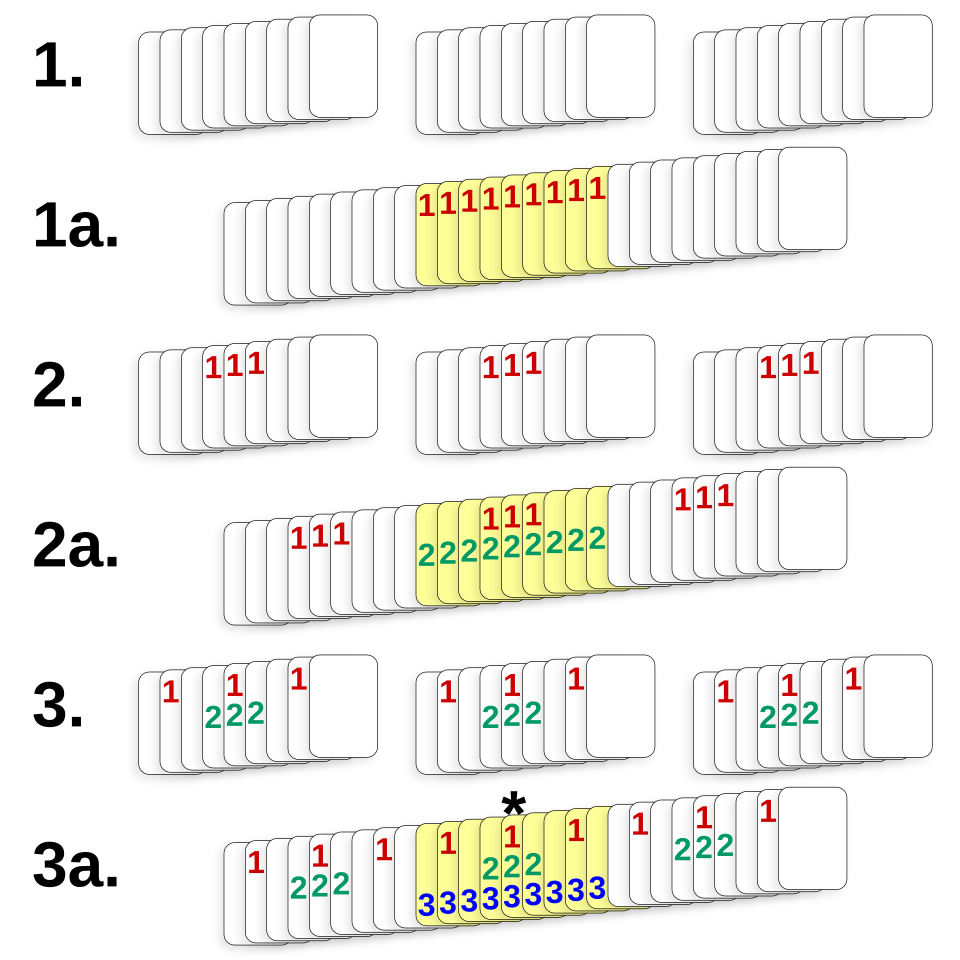
A performer takes 21 cards from a standard deck and shuffles them. A player notes one at random. The performer deals out the cards into three columns of seven cards each. The player indicates the column that contains her card. Twice more the performer deals out the cards into three columns and the player identifies the one containing her card. At this point the performer identifies the card.
How is this done? The trick works automatically so long as, in taking up the cards, the performer always puts the chosen pile between the other two. After the first deal, the chosen card will fall in one of positions 8-14; after the second deal, it will reach position 10-12; and after the last deal, it will be the 11th card in the assembled packet (at which point the performer can reveal it however he pleases).
This illustration, by CMG Lee, demonstrates the same principle using 27 cards. At each step, the pile containing the chosen card is shaded yellow; the numbers correspond to the step numbers. In this case the chosen card always finds its way to the 14th position.
Here’s an animation with 21 cards, in which the chosen card, marked with an X, finds its way to the 11th position:

A gigantic tire, with a radius of 100 miles, is rolling down Broadway at 60 mph. One driver fails to notice the tire’s approach until its descending surface is just touching the roof of her car, 6 feet above the road. If she leaves the car immediately and can shrink to within 2 feet of the road’s surface, how long does she have to crawl out of the tire’s path?

“Who knows if Shakespear might not have thought less, if he had read more?” — Edward Young
The Xmas Puzzles 2025 is now live — 13 fiendish puzzles and a “metapuzzle” that draws on their solutions. The competition will run until 20:00 GMT on January 18.
Quizmaster Tim Paulden has pledged just over £1000 in charitable donations as prizes. The top four entries will win a donation to a charity or good cause nominated by the solver: £200 for first place, £150 for second, £120 for third, and £90 for fourth. Those who solve the metapuzzle or score 50 percent or more will also win a donation.
Entry is free and open to all — participants can work alone or in teams of up to five people. Details are at the link above.

“Have you ever noticed … that all hot-water bottles look like Henry the Eighth?” — Max Beerbohm
Edmund Conti notes an unfortunate mannerism in Ngaio Marsh’s 1970 detective novel When in Rome:
Page 14: “Here,” he said in basic Italian. “Keep the change.” The waiter ejaculated with evident pleasure.
Page 49: “Nothing to what I was!” Sophy ejaculated.
Page 74: They could be heard ejaculating in some distant region.
Page 75: “Ah,” ejaculated Grant, “don’t remind me of that for God’s sake!”
Page 84: “Violetta, is it!” he ejaculated.
Page 87: “Good God!” the Major ejaculated.
Page 88: “Well!” the Major ejaculated.
Page 88: There were more ejaculations and much talk of coincidence …
Page 104: Marco gave an ejaculation and a very slight wince.
Page 109: “Phew!” said the Major, who seemed to be stuck with this ejaculation.
Page 140: “Eccellenza!” the Questore ejaculated.
Page 145: The Van der Veghels broke into scandalized ejaculations, first in their language and then in English.
Page 149: Sophy had given a little ejaculation.
Page 149: “I remember!” the Baron ejaculated.
Page 157: Finally Giovanni gave a sharp ejaculation.
Page 188: “We would exclaim, gaze at each at each other, gabble, ejaculate, tell each other how we felt …”
Page 194: Bergami ejaculated and answered so rapidly that Alleyn could only just make out what he said.
Conti adds, “Cigarette?”