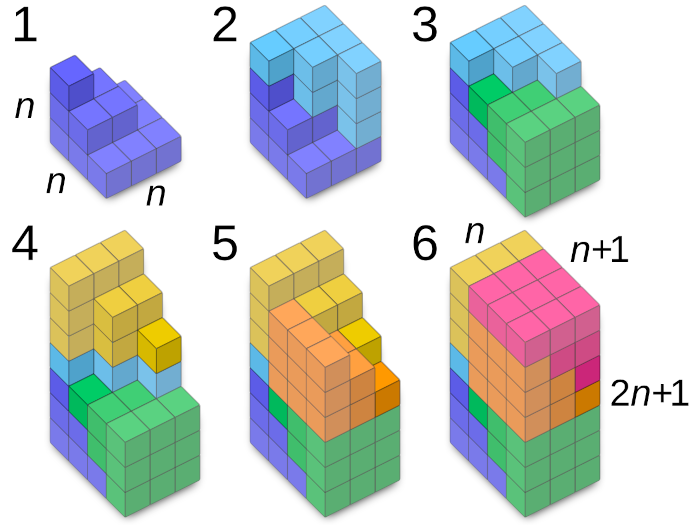
The sum of the first n square numbers is n(n+1)(2n+1)/6.

These sums comprise the square pyramidal numbers — each corresponds to the number of oranges that can be stacked in a square pyramid whose base has side n.

This visual proof, for n=3, shows that six square pyramids with n steps fit in a cuboid of size n(n + 1)(2n + 1).

(By CMG Lee.)