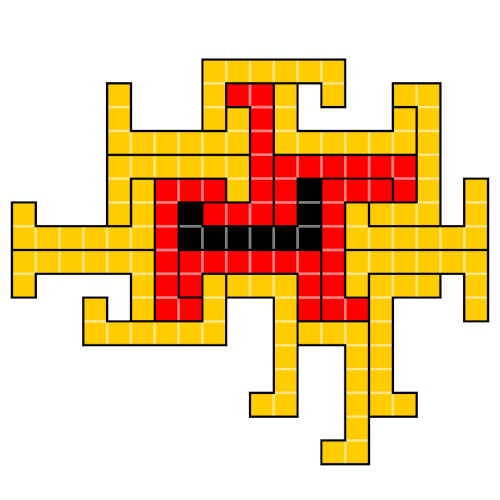
The dark polyomino at the center of this figure, devised by Craig S. Kaplan, has an unusual property: It can be surrounded snugly with copies of itself, leaving no overlaps or gaps. In this case, the “corona” (red) can be surrounded with a second corona (amber), itself also composed of copies of the initial shape. But that’s as far as we can get — there’s no way to create a third corona using the same shape.

That gives the initial shape a “Heesch number” of 2 — the designation is named for German geometer Heinrich Heesch, who had proposed this line of study in 1968.

Shapes needn’t be polyominos: Heesch himself devised the example below, the union of a square, an equilateral triangle, and a 30-60-90 triangle:

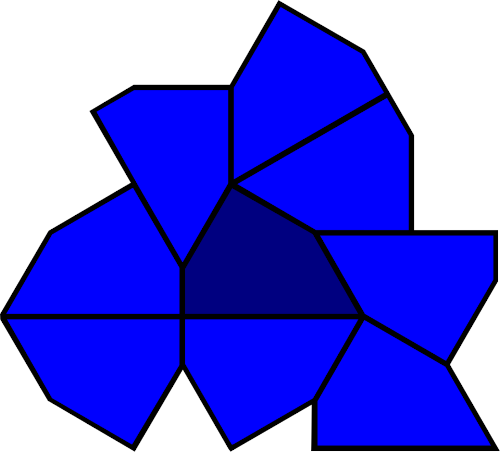
It earns a Heesch number of 1, as it can bear only the single corona shown.

Can all positive integers be Heesch numbers? That’s unknown. The Heesch number of the square is infinite, and that of the circle is zero. The highest finite number reached so far is 6.