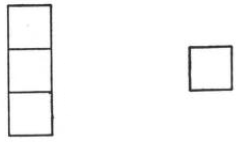
A tromino is a domino of three panels in a row, sized to cover three successive orthogonal squares of a checkerboard.
A monomino covers one square.
Is it possible to cover an 8×8 checkerboard with 21 trominoes and 1 monomino?
|
SelectClick for Answer |
Yes. Color the board’s squares like so:

This gives us 22 gray, 21 black, and 21 white squares. We can accomplish our task if each tromino covers squares of three different colors.
Where shall we put the monomino? It can’t go in the bottom left square, for example, as that would leave us with 22 gray, 21 white, and 20 black squares. By symmetry we can also reject the board’s three other corner squares, which might equally well have been colored black, ruining our plan by the same reasoning.
Extending this idea, the monomino can’t go on any white or black square or on any square symmetric to a white or black square. Of the 22 gray squares on the board, only four are symmetric only to other gray squares. If the monomino is placed on one of these squares, the remainder of the board can be covered with 21 trominoes. A sample tiling is shown below.
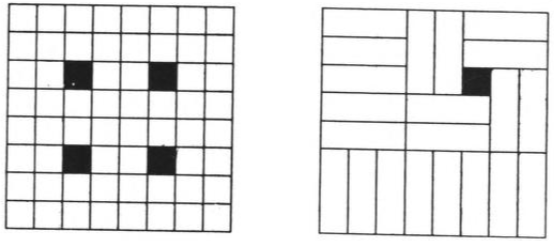
From J.A.H. Hunter and Joseph S. Madachy, Mathematical Diversions, 1963.
|

