In his Canterbury Puzzles of 1907, Henry Dudeney posed a now-famous challenge: How can you cut an equilateral triangle into four pieces that can be reassembled to form a perfect square?

Dudeney’s beautiful solution was accompanied by a rather involved geometric derivation. It seems unlikely that he worked this out laboriously in approaching an answer to the problem, but how then did he reach it?

Here’s one possibility: If a strip of squares is draped adroitly over a strip of triangles, their intersection forms a wordless proof of the task’s feasibility:

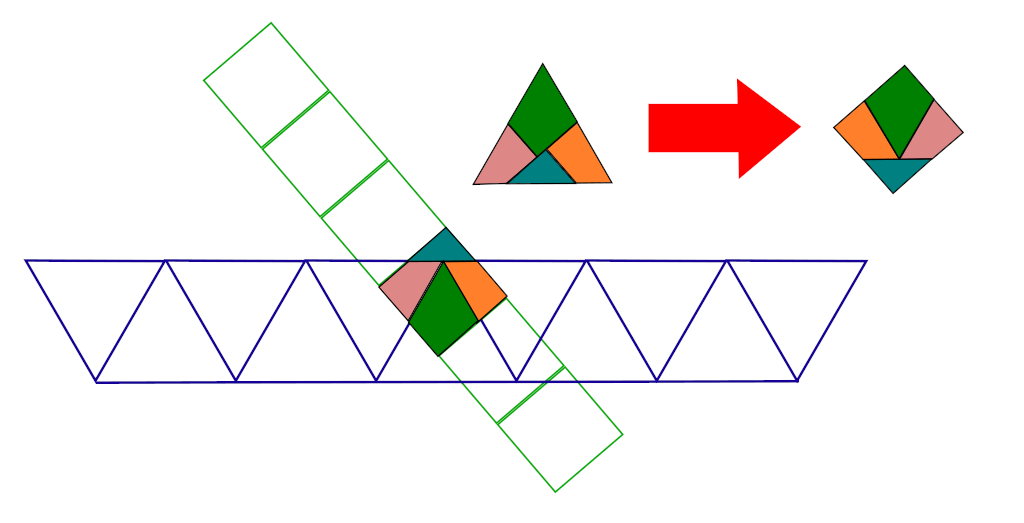
Whether that was Dudeney’s path to the solution is not known, but it appears at least plausible.