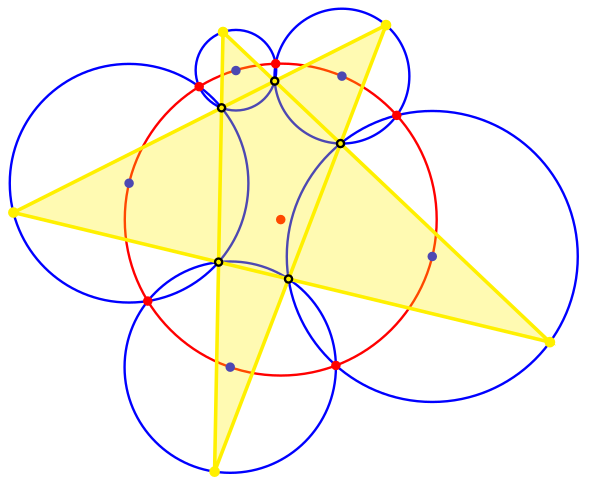
Draw a pentagram and enclose its arms in circles as shown. Each pair of adjoining circles will intersect at two points, one at a juncture of the pentagram’s arms. The second points of intersection will lie on a circle.

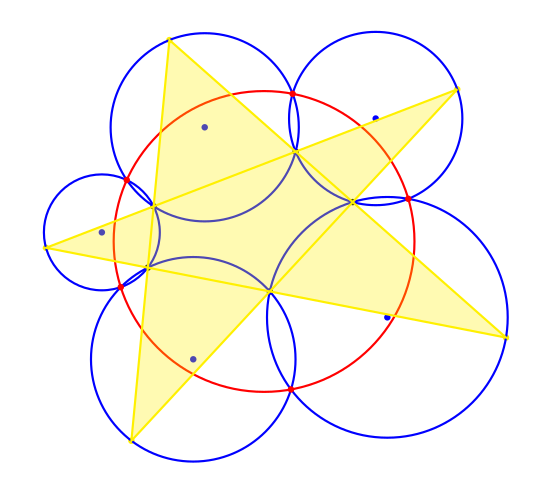
The converse is true if the centers of the five circles lie on that implied (red) circle (below): The lines connecting the second intersection points of neighboring circles will describe a pentagram whose outer vertices fall on the circles.

Discovered by Auguste Miquel.