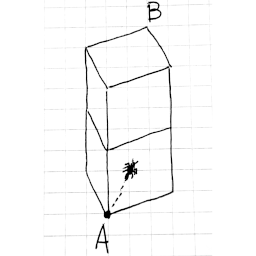
An inquisitive ant sets out from point A at a bottom vertex of the 1 × 1 × 2 box shown above. Of all the possible destinations it might seek in a direct route along the surface of the box, which one requires the longest journey?

Intuitively we might think it’s point B, the farthest vertex on the box roof. But Japanese mathematician Yoshiyuki Kotani discovered that the longest journey actually ends one-fourth of the way along the rooftop diagonal that ends at point B.

This can be seen by “unfolding” the box into a flat diagram, where four different paths can be traced from A to that point. The Pythagorean theorem shows that all four paths have the same length, 2.850…, which is about 0.022 longer than the shortest path to B.

Data scientist Shiro Matsumoto provides some animations here.

(Martin Gardner, “The Ant on a 1 × 1 × 2,” Math Horizons 3:3 [February 1996], 8-9.)