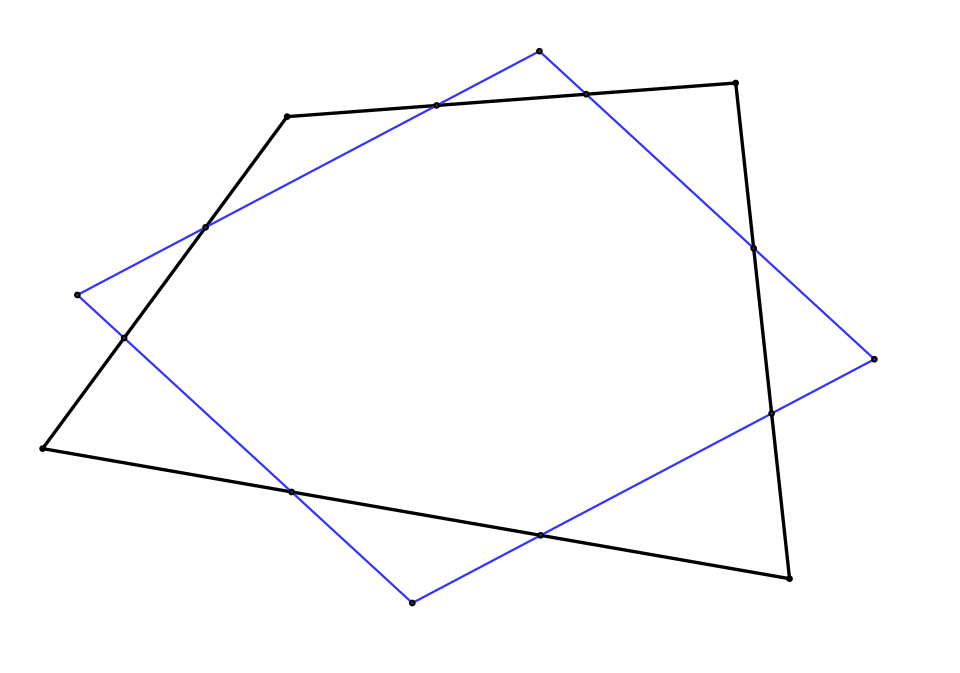
Draw an arbitrary quadrilateral and divide each of its sides into three equal parts. Draw a line through adjacent points of trisection on either side of each vertex and you’ll have a parallelogram.

Discovered by Austrian engineer Ferdinand Wittenbauer.

07/03/2025 UPDATE: Reader Ross Ogilvie writes, “I realized that there is nothing special about dividing the sides into thirds. The construction still works so long as the two points adjacent to a vertex divide their respective sides in the same ratio. This ensures that the line connecting the adjacent points are parallel to a diagonal of the quadrilateral. In Wittenbauer’s construction, they divide the sides 1:2. The case of 1:1, so all the points are midpoints, is Varignon’s theorem. It’s even possible that different vertices have different ratios. I drew up a little demo if you would like to play around and see for yourself. Move the sliders a,b,c,d to change the ratios.”