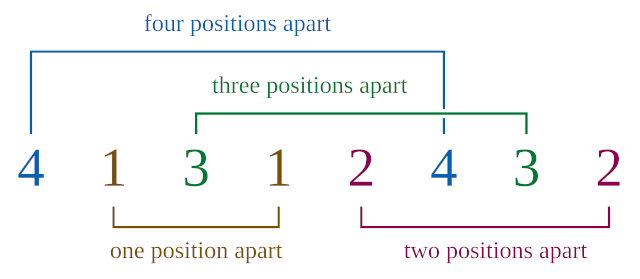
In the 1950s, mathematician C. Dudley Langford was watching his son play with blocks, two of each color, when he noticed that they formed a curious pattern: one block lay between the red blocks, two between the blue blocks, and three between the yellow blocks. Langford found that by rearranging the blocks he could add a green pair with four blocks between them.

This presented a clear challenge. He found solutions for as many as 15 pairs of blocks but came to believe that some smaller groupings (14 pairs, for example) could not produce a solution. He asked for a general investigation.

Today we know that a solution exists if and only if the number of blocks is 4k or 4k + 3, so Langford was right that no solution can be arranged with 14 pairs of blocks. The number of solutions for each quantity of pairs is listed here, and a few proofs are given here.

(C. Dudley Langford, “Problem,” Mathematical Gazette 42:341 [October 1958], 228.)