A puzzle by James M., an operations researcher at the National Security Agency:
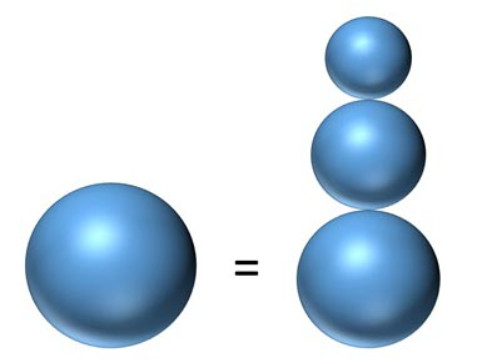
Frosty the Snowman wants to create a small snowman friend for himself. The new snowman needs a base, torso, and a head, all three of which should be spheres. The torso should be no larger than the base and the head should be no larger than the torso.
For building material, Frosty has a spherical snowball with a 6-inch radius. Since Frosty likes to keep things simple, he also wants the radius of each of the three pieces to be a positive integer. Can Frosty accomplish this?
|
SelectClick for Answer |
Yes! The formula for the volume of a sphere with radius r is 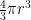 . Let a, b and c be the radii of the base, torso, and head, respectively, which are integers greater than 0. The problem then amounts to Frosty solving the equation . Let a, b and c be the radii of the base, torso, and head, respectively, which are integers greater than 0. The problem then amounts to Frosty solving the equation
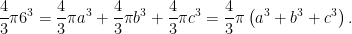
By canceling out the factor of  from both sides, we’re left with from both sides, we’re left with

As stated in the problem, a ≥ b ≥ c. The biggest that a can be is 5, so let’s try that first. Subtracting 53 = 125 from both sides gives us
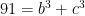
The biggest that b can be is 4, so let’s try that next. Subtracting 43 = 64 from both sides gives us
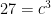
Frosty is in luck, since 33 = 27. Thus we have that 63 = 53 + 43 + 33. Now Frosty can build his new snowman friend to his specifications. In fact, (5, 4, 3) is the only combination of numbers that will work.
From NSA’s Puzzle Periodical series.
|

