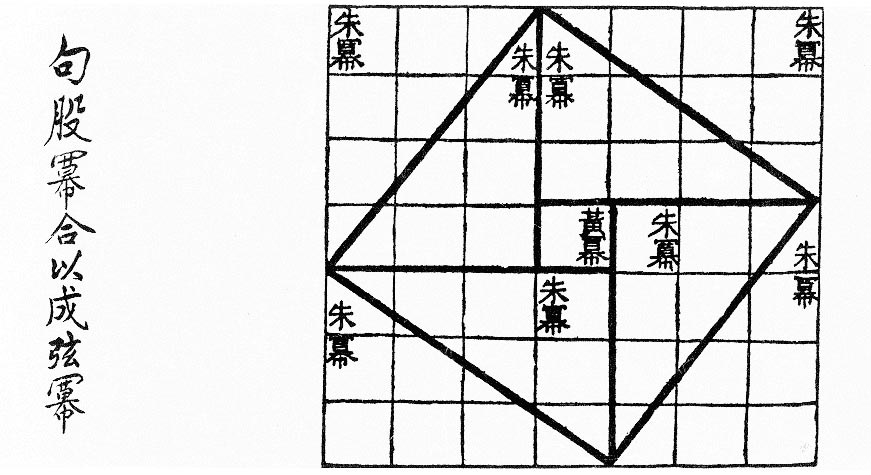
As early as the 1st century B.C., the Chinese text Zhou Bi Suan Jing reflected the reasoning of the Pythagorean theorem, showing how to find the hypotenuse of the 3-4-5 triangle. Arrange four 3×4 rectangles around a unit square, as shown, producing a 7×7 square. The diagonals of the four rectangles produce a tilted square. Now, the area of the 7×7 square is 49, and the area of one right triangle with legs 3 and 4 is 6. So the area of the tilted square is 49 – (4 × 6), or 25. This shows that the hypotenuse of each of the right triangles is 5.
In Mathematics and the Aesthetic (2007), Nathalie Sinclair writes, “The Chinese diagram … is the same as one given by the twelfth-century Indian scholar Bhaskara, whose one-word injunction Behold! recorded his sense of awe.”
