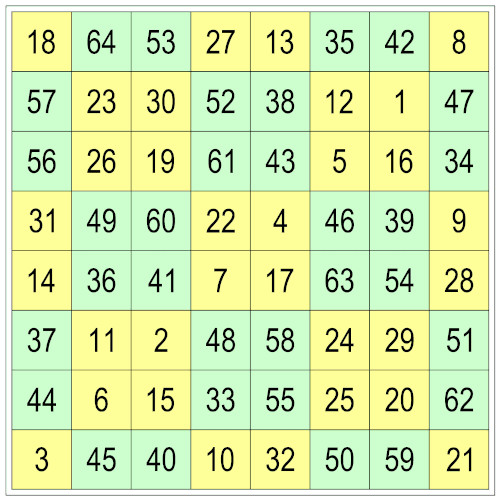
A queen’s tour is the record of a chess queen’s journey around an empty board in which she visits each of the squares once. If the squares are numbered by the order in which she visits them, then the resulting square is magic if the numbers in each rank and file sum to the same total. It’s bimagic if the squares of these numbers also produce a consistent total.
William Walkington has just found the first bimagic queen’s tour, which also appears to be the first bimagic tour of any chess piece. (William Roxby Beverley published the first magic knight’s tour in The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science in 1848.)
Note that here the long diagonals don’t produce the magic sum, as they would in a magic square. This constraint is normally dropped in a magic tour — in fact, of the 140 magic knight tours possible on an 8×8 board, none have two long magic diagonals, and no bimagic queen’s tour with qualifying diagonals is possible on such a board either.
More details, and an interesting description of the search, are on William’s blog. He has been told that a complete list of such bimagic queen’s tours is within reach of a computer search, though the field is daunting — there are more than 1.7 billion essentially different semi-bimagic squares possible on an 8×8 board, and each allows more than 400 million permutations.
