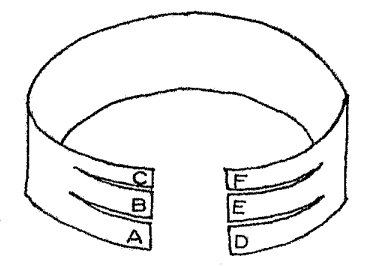
Most people know that if you cut a Möbius band in two lengthwise you’ll produce one band rather than two. But splitting the ends and joining them also creates some surprising effects.
Starting with the figure above, join ends A and D directly, then pass B under A and join it to E. Now pass C over B and under A; pass F over D and under E; and join C and F. Extend the slits along the length of the band and you’ll have three linked rings.
Now compare this variant, suggested by Ellis Stanyon in 1930: Starting again from the diagram, give E a half-twist to the right and join it to C; give F a half-twist to the right and join it to B; then pass A under B and join it to D (without turning it over). Cut along the two slits and you’ll produce a small ring linked to a large one. What became of the third ring?
There’s a surprisingly simple way to produce a similar effect: Draw a line along the length of a Möbius band, one-third of the way across the strip. Cutting along this line will produce a large band linked to a small one — and this time the small band is itself a Möbius band, on which you can repeat the feat.
