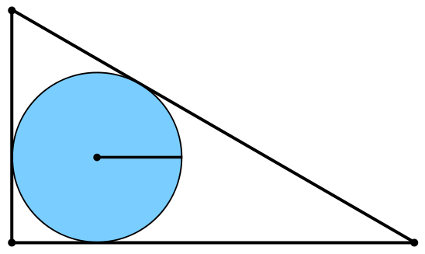
The radius of a circle inscribed in a 3-4-5 triangle is 1.
(In fact, the inradius of any Pythagorean triangle is an integer.)

The radius of a circle inscribed in a 3-4-5 triangle is 1.
(In fact, the inradius of any Pythagorean triangle is an integer.)
“It is not titles that honor men, but men that honor titles.” — Machiavelli

In 1930 Harold Lasseter claimed he’d discovered an enormous deposit of gold in the remote interior of Australia, and a small group of men set off into the punishing desert in search of a fortune estimated at 66 million pounds. In this week’s episode of the Futility Closet podcast we’ll tell the story of Lasseter’s reef, one of the most enduring legends of the Australian outback.
We’ll also reconsider the mortality rates of presidents and puzzle over an unlocked door.

All new ventures have their detractors, and James had his full share with the Cavendish project. One diminishing but still powerful school of critics held that, while experiments were necessary in research, they brought no benefit to teaching. A typical member was Isaac Todhunter, the celebrated mathematical tutor, who argued that the only evidence a student needed of a scientific truth was the word of his teacher, who was ‘probably a clergyman of mature knowledge, recognised ability, and blameless character’. One afternoon James bumped into Todhunter on King’s Parade and invited him to pop into the Cavendish to see a demonstration of conical refraction. Horrified, Todhunter replied: ‘No, I have been teaching it all my life and don’t want my ideas upset by seeing it now!’
— Basil Mahon, The Life of James Clerk Maxwell, 2004
In December 1968, kidnappers abducted 20-year-old university student Barbara Jane Mackle from her family’s home in Coral Gables, Fla., drove her to a remote pine stand near Norcross, Ga., and buried her in a box. Inside she found this message:
DO NOT BE ALARMED. YOU ARE SAFE.
YOU ARE PRESENTLY INSIDE A FIBERGLASS REINFORCED PLYWOOD CAPSULE BURIED BENEATH THE GROUND NEAR THE HOUSE IN WHICH YOUR KIDNAPPERS ARE STAYING. YOUR STATUS WILL BE CHECKED APPROXIMATELY EVERY 2 HOURS.
THE CAPSULE IS QUITE STRONG, YOU WILL NOT BE ABLE TO BREAK IT OPEN. BE ADVISED, HOWEVER, THAT YOU ARE BENEATH THE WATER TABLE. IF YOU BREAK OPEN A SEAM YOU WOULD DROWN BEFORE WE COULD DIG YOU OUT. THE CAPSULE INSTRUMENTATION CONTAINS A WATER SENSITIVE SWITCH WHICH WILL WARN US IF THE WATER ENTERS THE CAPSULE TO A DANGEROUS DEGREE.
YOUR LIFE DEPENDS ON THE AIR DELIVERED TO YOUR CHAMBER VIA THE VENTILATION FAN. THIS FAN IS POWERED BY A LEAD-ACID STORAGE BATTERY CAPABLE OF SUPPLYING THE FAN MOTOR WITH POWER FOR 270 HOURS. HOWEVER, THE USE OF THE LIGHT AND OTHER SYSTEMS FOR ONLY A FEW HOURS COUPLED WITH THE HIGHER AMPERAGE DRAIN WILL REDUCE THIS FIGURE TO ONLY ONE WEEK OF SAFETY.
SHOULD THE AIR SUPPLIED PROVE TO BE TOO MUCH YOU CAN PARTLY BLOCK THE AIR OUTLET WITH A PIECE OF PAPER. A MUFFLER HAS BEEN PLACED IN THE AIR PASSAGE TO PREVENT ANY NOISE YOU MAKE FROM REACHING THE SURFACE: IF WE DETECT ANY COMMOTION WHICH WE FEEL IS DANGEROUS, WE WILL INTRODUCE ETHER TO THE AIR INTAKE AND PUT YOU TO SLEEP.
THE FAN OPERATES ON 6 VOLTS. IT HAS A SWITCH WITH TWO POSITIONS TO SWITCH BETWEEN THE TWO AVAILABLE CIRCUITS. SHOULD ONE CIRCUIT FAIL TURN TO THE OTHER.
THE BOX HAS A PUMP WHICH WILL EVACUATE ANY ACCIDENTAL LEAKAGE FROM THE BOX WHEN YOU TURN THE PUMP SWITCH ON TO THE “ON” POSITION. THIS PUMP USES 15 TIMES AS MUCH POWER AS YOUR VENTILATION FAN (7.5 AMPS); YOUR LIFE SUPPORT BATTERY WILL NOT ALLOW USE OF THE PUMP EXCEPT FOR EMERGENCY WATER EVACUATION.
THE LIGHT USES 2.5 TIMES THE AMPERAGE OF THE AIR CIRCULATION SYSTEM. USE OF THE LIGHT WHEN NOT NECESSARY WILL CUT YOUR BATTERY SAFETY MARGIN SUBSTANTIALLY. IF YOU USE THE LIGHT CONTINUOUSLY YOUR LIFE EXPECTANCY WILL BE CUT TO ONE THIRD OF THE WEEK WE HAVE ALLOTTED YOU BEFORE YOU ARE RELEASED.
YOUR CAPSULE CONTAINS A WATER JUG WITH THREE GALLONS OF WATER AND A TUBE FROM WHICH TO DRINK IT. BE CAREFUL TO BLOW THE WATER FROM THE TUBE WHEN YOU ARE FINISHED DRINKING TO AVOID SIPHONING THE WATER ONTO THE FLOOR WHEN THE TUBE END DROPS BELOW THE WATER LEVEL.
YOUR CAPSULE CONTAINS A BUCKET FOR REFUSE AND THE PRODUCTS OF YOUR BOWEL MOVEMENTS. THE BUCKET HAS AN ANTIBACTERIAL SOLUTION IN IT: DON’T TIP IT OVER. THE LID SEALS TIGHTLY TO PREVENT THE ESCAPE OF ODORS. A ROLL OF WAX PAPER IS PROVIDED – USE IT TO PREVENT SOLID WASTE FROM CONTAMINATING YOUR BED. KOTEX IS PROVIDED SHOULD YOU NEED IT.
BLANKETS AND A MAT ARE PROVIDED. YOUR WARMTH DEPENDS ON BODY HEAT SO REGULATE THE AIR TO PREVENT LOSS OF HEAT FROM THE CAPSULE.
A CASE OF CANDY IS PROVIDED TO FURNISH ENERGY TO YOUR BODY.
TRANQUILIZERS ARE PROVIDED TO AID YOU IN SLEEPING – THE BEST WAY YOU HAVE TO PASS THE TIME.
THE VENTILATION SYSTEM IS DOUBLY SCREENED TO PREVENT INSECTS OR ANIMALS FROM ENTERING THE CAPSULE AREA. YOU RISK BEING EATEN BY ANTS SHOULD YOU BREAK THESE PROTECTION SCREENS.
THE ELECTRICAL COMPONENTS BEHIND THESE SCREENS ARE DELICATE AND THEY SUPPORT YOUR LIFE. DON’T ATTEMPT TO TOUCH THESE CIRCUITS.
WE’RE SURE YOUR FATHER WILL PAY THE RANSOM WE HAVE ASKED IN LESS THAN ONE WEEK. WHEN YOUR FATHER PAYS THE RANSOM WE WILL TELL HIM WHERE YOU ARE AND HE’LL COME FOR YOU. SHOULD HE FAIL TO PAY WE WILL RELEASE YOU, SO BE CALM AND REST – YOU’LL BE HOME FOR CHRISTMAS ONE WAY OR THE OTHER.
The kidnappers demanded $500,000 from Mackle’s father, a wealthy Florida land developer. While he was arranging a ransom drop, the FBI identified the lead kidnapper as Gary Steven Krist of the University of Miami. When he received the money, Krist called the FBI and gave directions to the box, where Mackle had spent 83 hours underground. When agents tore it open she said, “You’re the handsomest men I’ve ever seen.”
The kidnappers were quickly captured. Krist was sentenced to life in prison, and his accomplice, Ruth Eisemann-Schier, got seven years.
(From Hank Messick and Burt Goldblatt, Kidnapping: The Illustrated History, 1974.)
Dispensationalist pastor Clarence Larkin illustrated his books with intricate charts interpreting prophecy and explaining God’s action in history.
“[T]he charts had to be thought out and developed under the direction and guidance of the Holy Spirit,” he wrote in Dispensational Truth (1920). “In this the Holy Spirit did not confuse the Author by suggesting all the charts at one time. When one was completed another was suggested. And upon more than one occasion when a problem arose the answer was given in the night or at awakening in the morning.”
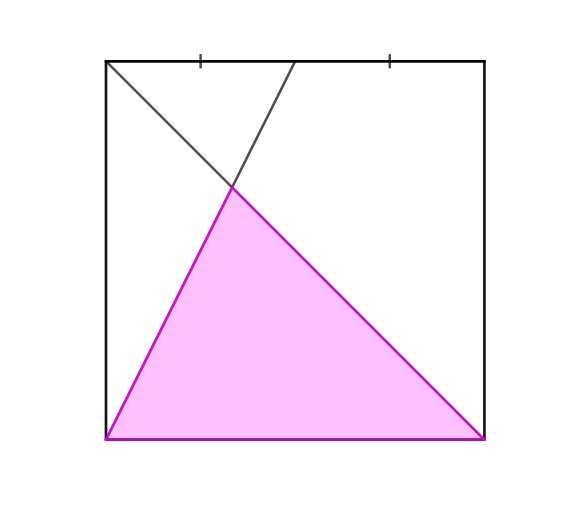
I think this appeared originally in Ed Southall’s Twitter feed. What fraction of the square is shaded?
The town of Glacier View, Alaska, doesn’t get dark enough for fireworks on the Fourth of July. So they drive cars off a cliff.
From Linda Zagzebski, Philosophy of Religion, quoted in W. Jay Wood, God, 2011.
There are 8 ways to fold a 2 × 2 map along its creases:
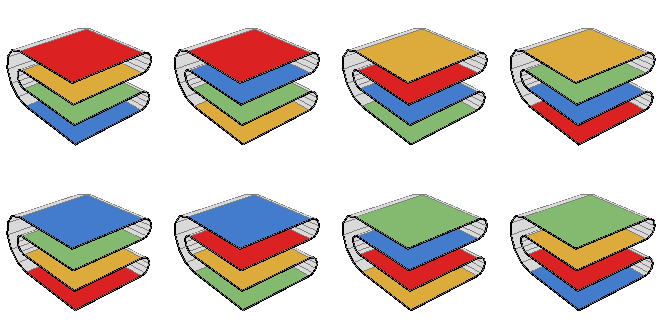
But no one knows how to calculate the number of ways that a larger map might be folded. Amazingly, the number of ways to fold an n × n map has been worked out only as high as 7 × 7:
1, 8, 1368, 300608, 186086600, 123912532224, 129950723279272
Via Fermat’s Library.