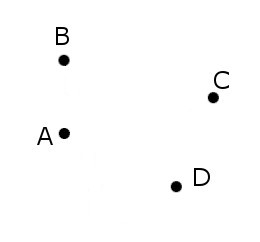
A “coffin,” or killer problem, from the oral entrance exams to the math department of Moscow State University:
Construct (with ruler and compass) a square given one point from each side.
|
SelectClick for Answer |
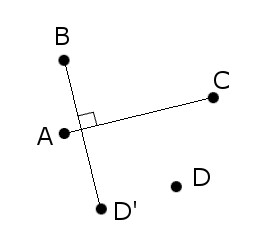
If A, B, C, and D denote the four points, connect A and C and draw a perpendicular from B to this segment. Let D’ lie on this perpendicular such that AC = BD’. Now D’ lies on the same side of the square (or on an extension of that side) as D. Connecting D and D’ gives us the orientation of the square, and the rest is easy.
According to Tanya Khovanova and Alexey Radul, in the 1970s such problems were cultivated expressly to prevent Jews and other undesirable students from entering the university. The challenging nature of the problems prevented students from solving them, and the existence of a simple solution gave cover to the administration. For further examples, see http://arxiv.org/pdf/1110.1556v1.pdf.
|

