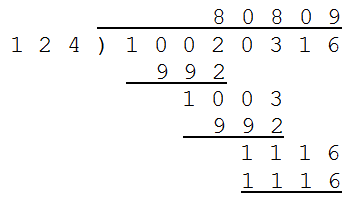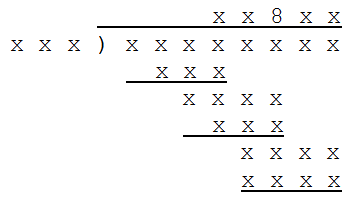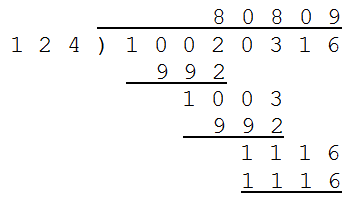In long division, whenever two digits are brought down instead of one — as happens twice in this problem — a zero must appear in the quotient. That tells us that the quotient is x080x.

The visible 8 multiplied by the divisor produces a three-digit number. But when the last number in the quotient is multiplied by the divisor, it produces a four-digit number. So the last digit in the quotient must be 9.

The divisor has three digits and produces a three-digit number when multiplied by the visible 8. So the divisor must be less than 125, because 8 × 125 = 1000.

That tells us something further. When the divisor is multiplied by the first digit of the quotient, it produces a three-digit number, and when this is subtracted from the first four digits of the dividend it yields a two-digit difference. That means that the first digit of the quotient must be greater than 7, because 7 × 124 = 868, and that would yield a three-digit difference when subtracted from even the smallest possible four-digit number, 1000 (1000 – 868 = 132). An 8 or a 9 could produce a two-digit difference, but a 9 would produce a four-digit number when multiplied by the divisor. So the first digit of the quotient is 8, and the full quotient is 80809.

Now, 80809 × 123 = 9939507, which has only seven digits, and the dividend has eight. So the divisor is less than 125 and greater than 123, which means it’s 124. That gives us everything we need: